Case Study: Verified Mobile Robots and Surgical Robots

Table of Contents
Obstacle Avoidance for Mobile Robots Surgical Robots for Skull-base Surgery Selected Publications

Obstacle Avoidance for Mobile Robots

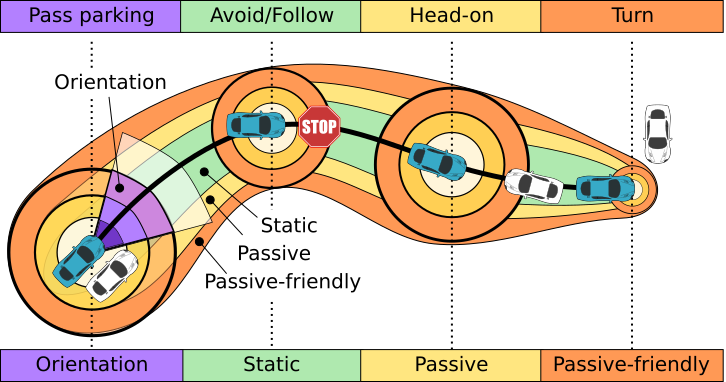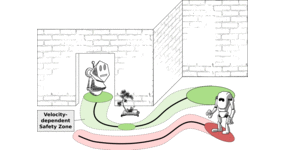We answer fundamental safety questions for ground robot navigation [3]: Under which circumstances does which control decision make a ground robot safely avoid obstacles? Unsurprisingly, the answer depends on the exact formulation of the safety objective as well as the physical capabilities and limitations of the robot and the obstacles. Because uncertainties about the exact future behavior of a robot's environment make this a challenging problem, we formally verify corresponding controllers and provide rigorous safety proofs justifying why they can never collide with the obstacle in the respective physical model. To account for ground robots in which different physical phenomena are important, we analyze a series of increasingly strong properties of controllers for increasingly rich dynamics and identify the impact that the additional model parameters have on the required safety margins.

We analyze and formally verify: (i) static safety, which ensures that no collisions can happen with stationary obstacles, (ii) passive safety, which ensures that no collisions can happen with stationary or moving obstacles while the robot moves, (iii) the stronger passive friendly safety in which the robot further maintains sufficient maneuvering distance for obstacles to avoid collision as well, and (iv) passive orientation safety, which allows for imperfect sensor coverage of the robot, i.e., the robot is aware that not everything in its environment will be visible. We formally prove that safety can be guaranteed despite sensor uncertainty and actuator perturbation. We complement these provably correct safety properties with liveness properties: we prove that provably safe motion is flexible enough to let the robot navigate waypoints and pass intersections. In order to account for the mixed influence of discrete control decisions and the continuous physical motion of the ground robot, we develop corresponding hybrid system models and use differential dynamic logic theorem proving techniques to formally verify their correctness. Since these models identify a broad range of conditions under which control decisions are provably safe, our results apply to any control algorithm for ground robots with the same dynamics.

Surgical Robots for Skull-base Surgery

. We applied quantified differential-dynamic logic (QdL) to analyze a control algorithm designed to provide directional force feedback for a surgical robot [1]. We identified problems with the algorithm, proved that it was in general unsafe, and described exactly what could go wrong. We then applied QdL to guide the development of a new algorithm that provides safe operation along with directional force feedback. Using KeYmaeraD (a tool that mechanizes QdL), we created a machine-checked proof that guarantees the new algorithm is safe for all possible inputs.

Selected Publications

Also see publications on verification of automotive systems.

1. Stefan Mitsch, Khalil Ghorbal, David Vogelbacher, and André Platzer.
   Formal verification of obstacle avoidance and navigation of ground robots.
   International Journal of Robotics Research 36(12), pp. 1312-1340, 2017. © The authors
   [bib | ⧉ | pdf | doi | kyx | arXiv | abstract]
   
   
2. Stefan Mitsch, Khalil Ghorbal and André Platzer.
   On provably safe obstacle avoidance for autonomous robotic ground vehicles.
   In Paul Newman, Dieter Fox, and David Hsu, editors, Robotics: Science and Systems, RSS 2013. © The author
   [bib | ⧉ | pdf | eprint | slides | video | study | IJRR'17 | abstract]
   
   
3. Yanni Kouskoulas, David W. Renshaw, André Platzer and Peter Kazanzides.
   Certifying the safe design of a virtual fixture control algorithm for a surgical robot.
   In Calin Belta and Franjo Ivancic, editors, Hybrid Systems: Computation and Control (part of CPS Week 2013), HSCC'13, Philadelphia, PA, USA, April 8-13, 2013, pp. 263-272. ACM, 2013. © ACM
   [bib | ⧉ | pdf | doi | slides | study | abstract]