Proving Theorems for
|
|

|
Find at Springer by DOI |
Reviews
|
"This book describes a truly unique approach to hybrid systems verification with logic and theorem proving."
(Edmund M. Clarke, Carnegie Mellon University)
|
Book Review Form. Asp. Comp. |
- Book Reviews:
- Fontana, G. P. Book review: Logical Analysis of Hybrid Systems. Form. Asp. Comp.. Formal Methods Europe, Book Reviews, 2020-11-24.
About the Author
| The author is an assistant professor in the Computer Science Department at Carnegie Mellon University. He has an M.Sc. in computer science from the University of Karlsruhe, Germany and a Ph.D. in computer science from the University of Oldenburg, Germany. Among other awards he won best paper awards at the Tableaux 2007 and FM 2009 conferences, he was among Popular Science Magazine's annual "Brilliant 10" in 2009, he received the ACM Doctoral Dissertation Honorable Mention Award in 2009, he was among the IEEE Intelligent Systems' biennial "AI's 10 to Watch" in 2011, and he received an NSF Career award in 2011. His research interests include the logical foundations of cyber-physical systems, theorem proving and model checking. | ACM Award |
| Brilliant 10 Award | |
| AI 10 Award |
Description
Hybrid systems are models for complex physical systems and have become a widely used concept for understanding their behaviour. Many applications are safety-critical, including car, railway, and air traffic control, robotics, physical-chemical process control, and biomedical devices. Hybrid systems analysis studies how we can build computerised controllers for physical systems which are guaranteed to meet their design goals.
This is the first book that leverages the power of logic for hybrid systems. The author develops a coherent logical approach for systematic hybrid systems analysis, covering its theory, practice, and applications. It is further shown how the developed verification techniques can be used to study air traffic and railway control systems.
This book is intended for researchers, postgraduates, and professionals who are interested in hybrid systems analysis, cyber-physical or embedded systems design, logic and theorem proving, or transportation and automation.
Table of Contents
| Part I Logics and Proof Calculi for Hybrid Systems |
See Full Table of Contents |
| Part II Automated Theorem Proving for Hybrid Systems Part III Case Studies and Applications in Hybrid Systems Verification Part IV Appendix | |
Where to Get This Book
|
The book has appeared with Springer under ISBN 978-3-642-14508-7. Find
|
Look at Book Flyer |
Online Material
|
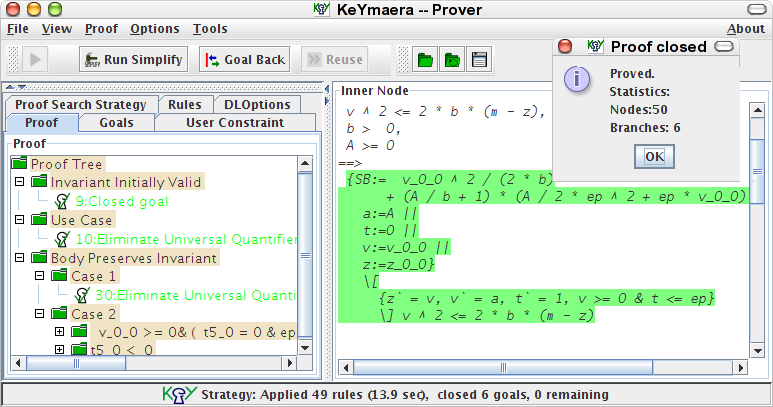
There is a verification tool implementing the approach described in this book. This verification tool for hybrid systems is called KeYmaera and is available for installation.
|
Operators
and Rules |
Bibliographic Information
This book has appeared with Springer [1].-
André Platzer.
Logical Analysis of Hybrid Systems:
Proving Theorems for Complex Dynamics.
Springer, Heidelberg, 2010. 426 pages. ISBN 978-3-642-14508-7.
[bib | ✂ | doi | book | web | errata | abstract]
- Subject Index:
-
Mathematical Logic and Formal Languages
Artificial Intelligence and Robotics
Mathematics of Computing
Logics and Meanings of Programs
Control, Robotics, Mechatronics
|
André Platzer. Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics. Springer, 2010. 424 pages, ISBN 978-3-642-14508-7. Published 2010-09-07. DOI 10.1007/978-3-642-14509-4. |
 |